Physically Based Toon Shading in Unity

Technical Blog

Outline

The final demo scene

In this blog I will outline and discuss the different techniques used to create a more physically based approximation for toon shading in Unity. In a later blog entry I will detail techniques for calculating and rendering water that is appropriate to this rendering style.

The goal with this project was to create a “cel-shading” style toon shader that would behave in a predictable manner and provide approximate energy conservation like a physically based shader.

What is Toon Shading?

Cel shading or toon shading is a type of non-photorealistic rendering designed to make 3-D computer graphics appear to be flat by using less shading color instead of a shade gradient or tints and shades. Cel-shading is often used to mimic the style of a comic book or cartoon and/or give it a characteristic paper-like texture.

Cel-shading - Wikipedia

An example of toon or cel-shading

The key component of toon shading is that the lighting calculations are quantized or posterized to make lighting and shadow use only a few shades of flat color. In addition to this, lots of toon shaded games also apply an additive rim-light, which is not quantized, to soften the final image and help players identify the difference between objects subconsciously. The Legend of Zelda: The Wind Waker is a good example of this. Additionally, toon shaded games often draw outlines, whether by drawing backfaces first or by an edge detection filter such as a Sobel filter, although we will not be implementing that in this example.

The BSDF

A BSDF (or bidirectional scattering distribution function) is a formula used to describe how light is reflected by (BRDF) or transmitted through (BTDF) a surface. As I want these shaders to be efficient enough to run on mobile I will base the BRDF on the popular Blinn-Phong model and the BTDF on a wrap diffuse approximation. Whilst these approximations are by no means accurate by modern standards they will serve fine given how their output with be quantized anyway.

Specular Term

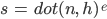
Blinn Phong

The basis for the Blinn Phong BRDF, pictured above, is the dot product of the normal vector (n) and the half vector (h) to the power of an exponent (e). The half vector here is an approximation of the reflection vector used in regular Phong shading.

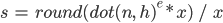
Stepped Blinn Phong

In our Toon Shading version we simply multiply the result of a regular Blinn Phong calculation by a step value (x), round the result, then divide by the same step value. This has the appearance of quantizing the specular value into the amount of values specified by the step value.

Step Value

Our step value (x) needs to be relative to the roughness value so as the specular highlight gets tighter the amount of steps drops. For this we use roughness (1 - smoothness) to the power of an exponent (e).

half specular  = normalize(dot(n, h));
half steps = max(((1 - smoothness) * 2), 0.01);
return round(specular * steps) / steps;

In HLSL this looks like the above code. However, in the actual implementation I use the same specular lookup as used in Unity’s default fallback Unity_BRDF3. This saves instructions and improves performance.

Diffuse Term

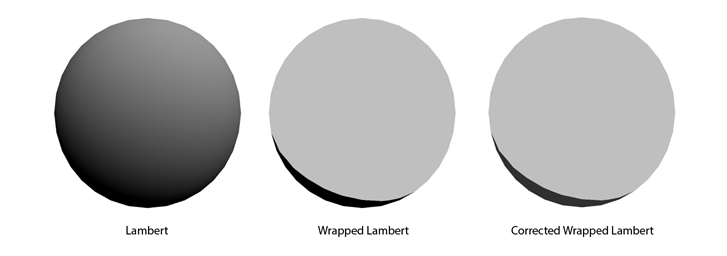
Wrapped Lambert

Because we want to simulate some transmission we will use the popular wrap lambertian model for the basis of our diffuse term. In the equation above the wrap term (w) is our transmission value.

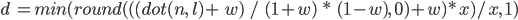
Corrected stepped Lambert

Because we want our diffuse to be boolean (either on or off) we will use the same technique as we did with the specular term of rounding with a step value, however we will use a fixed step value of 2. Because our step function removes the change in falloff, this approach has the effect of merely pushing the point of shadow away from the direction of the light source. To create a softer looking result at high transmission levels I then add the transmission value to the output and clamp it to one. This helps prevent an extremely hard contrast at the point of shading.

float3 diffuse = saturate((dot(normal, lightDir) + w) / ((1 + w) * (1 + w)));
Float3 stepDiffuse = min(step(0.01, diffuse) + (w), 1);
return stepDiffuse * lightColor;

The final HLSL code looks like the above. This is the section of the BSDF where energy conservation breaks down. I simply haven’t found a way to get near energy conservation when stepping a wrapped diffuse term like this. In the future I would like to find a better way to model this.

Additional Fresnel Term

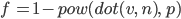
Traditional rim light

Like I stated in the introduction I wanted to add an additive fresnel to soften the overall visuals much like in Legend of Zelda: The Wind Waker. For this I used the popular fresnel model shown above, where v is view direction, n is normal direction and p is fresnel power.

This is then multiplied by the fresnel color. In my case I decided to interpolate between a mid grey color and the diffuse color for that pixel based on a diffuse contribution value defined by the user. Finally I apply a blend factor and a final tint color.

Final BSDF

There is nothing particularly special about the final BSDF composition. We calculate the same grazing term and indirect term as any other PBR shader in Unity. I chose not to do any post processing or alteration to the indirect term as if every shader sampled for indirect also uses a Toon shader than all the probe values should be appropriate for the shading already.

half grazingTerm = saturate(smoothness + (1 - oneMinusReflectivity)); // Calculate grazing term
half3 indirect = ToonBRDF_Indirect(diffColor, specColor, gi, grazingTerm, fresnelTerm); // Calculate indirect

// Compose output
half3 color = (diffColor + specular) * diffuse
    + fresnel
    + indirect;

return half4(color, 1); // Return

Finally we add the specular, fresnel and indirect terms to the diffuse term and return.

As with everything this is an ongoing project. If you have any comments or suggestions please get in contact by tweeting @matthewdean3d. Thanks for reading!